PROGRAM LINIER: METODE SIMPLEX
Persoalan program linier tidak selalu sederhana karena melibatkan banyak
constraint (pembatas) dan banyak variabel sehingga tidak mungkin
diselesaikan dengan metode grafik. Oleh karena itu serangkaian prosedur
matematik (aljabar linier) diperlukan untuk mencari solusi dari persoalan
yang rumit tersebut. Prosedur yang paling luas digunakan adalah Metode
Simplex. Penemuan metode ini merupakan lompatan besar dalam Riset Operasi
dan ia digunakan sebagai prosedur penyelesaian dari setiap program
komputer.
Bentuk Aljabar Metode Simplex
Silahkan klik link : http://mnc-cholis.blogspot.com/2011/09/program-linier-metode-simplex.html

 dalam 20 tempat desimal adalah 3,14159265358979323846. Atau yang lebih lengkap seperti di bawah ini
dalam 20 tempat desimal adalah 3,14159265358979323846. Atau yang lebih lengkap seperti di bawah ini






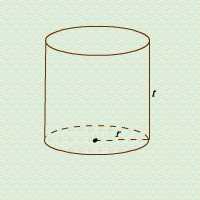 dengan:
dengan: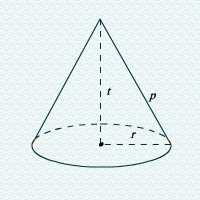 dengan:
dengan: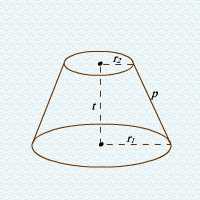 dengan:
dengan: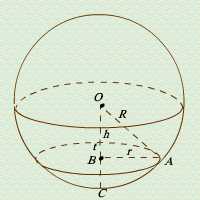 dengan:
dengan:

